7. Additive and Multiplicative Judgements of Dialectical Logic. Additive and multiplicative differentials and Integrals of Dialectical Judgements
L. G. Kreidik (translation from Russian T. S. Kortneva and G. P. Shpenkov)
7.1. Motators and fields of judgements
Opposites, describing objects of nature, and opposites, expressing the diversity of relations between them, represent a set of dialectical reflections consisting of descriptions, statements, judgements, and reasoning. If reflections are substituted by concrete quantitative-qualitative numbers and symbols-relations, they are transformed into a quantitative-qualitative dialectical set of measures-numbers. In this sense, reflections and numbers are two facets of the language of dialectics.
As sources of reflections, objects of nature will be called motators (from the Latin, motator=acting) and their fields will be named fields of judgements of relations and exchange. Logical images of the fields are described by fields of opposites. Motators and fields are closely interlaced into a whole contradictory complex of motator-field relations and exchange. Motators are, to some extent, generators and transformers of the fields of relations and exchange. They generate these fields and change themselves under their action. A simplest potentially-kinetic field of a judgement has the form
![]() ,
(1.145)
,
(1.145)
where ![]() is the judge'ment modulus,
is the judge'ment modulus, ![]() .
.
The number e is a basis of a harmonic unit and deserves special attention. In order to understand its profound meaning, the notions of a differential and a derivative will be expanded.
7.2. Additive and multiplicative continuity
Modern science explicitly operates by additive continuity.
In physics, additive continuity is expressed by the continuously variable sums.
For example, at uniform motion the passed distance S is the additive
continuity: ![]() .
.
Continuously variable sums are described by classical differentials, derivatives, and integrals, which will be called the additive differentials, derivatives, and integrals.
On the other hand, many processes are expressed via continuously
variable products by infinite products of factors of continuous series. These
judgements-products express multiplicative continuity. Simplest example of their
are the exponential functions ![]() ,
,
![]() ,dialectical judgements
of the kind (1.93), etc.
,dialectical judgements
of the kind (1.93), etc.
The classical mathematics expresses multiplicative continuity by additive differentials, derivatives and integrals. However, it is insufficient for the profound and comprehensive description of multiplicative continuity and for understanding its physical sense. In a general case, additive and multiplicative continuities are polar-opposed phenomena. Nevertheless, they are identified tacitly by mathematics. This occurs very often with the notions as motion and rest, although these phenomena are not equal each other.
On the level of formal logic, motion is usually considered as a infinite sum of rest states, but it does not correct. It is more rightly to describe motion by motion and rest by rest.As above, multiplicative differentials, derivatives and integrals should realize a more precise description of multiplicative continuity.
In the real World, additive and multiplicative continuities are united together in the one dialectical complex, namely, the additive-multiplicative continuity. It has to be described both the additive and multiplicative differentials, derivatives and integrals.
It is clear, the additively-multiplicative continuity is inseparable on the additively-multiplicative discontinuity, i.e. the additively-multiplicative sharp pulse transitions.
7.3. A multiplicative differential and derivative; the meaning of number "e"
A multiplicative ratio or multiratio ![]() between different states of the variable opposite
between different states of the variable opposite ![]() at the points
at the points ![]() and
and ![]() defines
the multiplicative differential of the judgement at the point
defines
the multiplicative differential of the judgement at the point ![]() :
:
![]() .
(1.146)
.
(1.146)
The multiplicative derivative![]() at the point t we define as the limit of the multiplicative ratio
of the multiratio
at the point t we define as the limit of the multiplicative ratio
of the multiratio ![]() to
the differential
to
the differential ![]() in the followingway:
in the followingway:
![]() , (1.147)
, (1.147)
where ![]() is a degree of the multiratio
is a degree of the multiratio ![]() .
.
Since ![]() ,
then
,
then
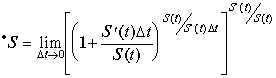 .
(1.148)
.
(1.148)
The expression in square brackets has the number e as the limit, therefore
![]() .
(1.149)
.
(1.149)
The multiplicative derivative will be written symbolically as
![]() .
(1.149a)
.
(1.149a)
Additive and multiplicative derivatives are related by the simple equality
![]() .
(1.150)
.
(1.150)
Returning back to limit (1.72), we conclude that the number e is a multiplicative derivative of a variable unit, describing multiplicative continuity:
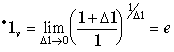 . (1.151)
. (1.151)
Using the formula (1.149), we find the multiplicative derivative
(1.151) of the variable unit of negation ![]() .
Since
.
Since ![]() , then
, then
![]() . (1.151a)
. (1.151a)
Evidently, the multiplicative derivative of a harmonic judgement of the unit amplitude with respect to j (see (1.99)) will be equal to
![]() .
(1.151b)
.
(1.151b)
Thus, it is inversely proportional to the multiplicative derivative of the variable unit of negation:
![]() .
(1.151c)
.
(1.151c)
The multiplicative derivative of the quantitative-qualitative harmonic unit of a judgement with respect to t (see (1.98)) has the form
![]() .
(1.151d)
.
(1.151d)
On the basis of (1.147) we express the multiplicative differential via the multiplicative derivative
![]() , (1.152)
, (1.152)
where ![]() is the degree of the multiplicative derivative with the exponent
is the degree of the multiplicative derivative with the exponent ![]() .
.
Thus,
![]() .
(1.152a)
.
(1.152a)
These relations, (1.152) and (1.152a), are similar to the corresponding additive relations
![]() ,
(1.153)
,
(1.153)
![]() .
(1.153a)
.
(1.153a)
We will represent here, for comparison, the additive and multiplicative derivatives of some elementary functions:
![]() ___
___ ![]()
![]() ___
___ ![]()
![]() ___
___ ![]()
![]() ___
___ ![]()
![]() ___
___ ![]()
_________ ![]() ___
___
![]() (1.154)
(1.154)
![]() ___
___ ![]()
![]() ___
___
![]()
![]() ___
___ ![]()
![]() ___
___
![]() .
.
It is known that an additive derivative of a function/ is determined as speed of its change. Analogously, a multiplicative derivative is multiplicative speed of multiplicative process change.
Let a harmonic judgement
![]() (1.155)
(1.155)
describes an elementary process. Its additive and multiplicative speeds are equal, respectively, to
![]() ,
,
![]() . (1.156)
. (1.156)
From here, we find correlation between these speeds
![]() .
(1.157)
.
(1.157)
Now the judgement can be written as
![]() .
(1.158)
.
(1.158)
This expression is an analog of an uniform additive process:
![]() (1.158a)
(1.158a)
where ![]() is a constant additive speed.
is a constant additive speed.
Therefore, it makes sense the expression (1.158) to call an uniform multiplicative process and its multiplicative speed as the uniform multiplicative speed. Thus, elementary harmonic oscillations of any nature are uniform multiplicative processes.
An additive speed of a harmonic judgement (1.155), being additively variable, is multiplicatively uniform according to (1.157). Consequently, a harmonic pulse of a material point of mass m is also multiplicatively uniform:
![]() (1.159)
(1.159)
where Pm is an pulse amplitude.
An additive acceleration during an uniform additive process is equal to zero. Whereas a multiplicative acceleration, as per (1.149) and (1.156) is equal to unit. It is easy to understand. In fact, zero does not change the constant additive process as well as unit does not change the constant multiplicative process.
The multiplicative speed of an unit judgement (1.98) is equal to the multiplicative speed of a harmonic judgement (1.155):
![]() .
(1.160)
.
(1.160)
hence, expressions (1.158) and (1.159) can be represented also in the form
![]() ,
,
![]() . (1.161)
. (1.161)
7.4. A multiplicative integral
Similarly to the additive definite integral
 (1.162)
(1.162)
we will determine the multiplicative definite integral equal to the limit of products of multiplicative ratios
![]() .
(1.162Ó)
.
(1.162Ó)
The indefinite additive integral with an additive constant C
![]() (1.163)
(1.163)
corresponds to the indefinite multiplicative integral with a multiplicative constant C
![]() .
(1.163a)
.
(1.163a)
On the basis of (1.149), we find relation between the multiplicative and additive definite integrals:
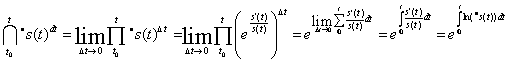 .
.
Thus, for definite and indefinite integrals we have
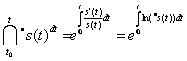 ,
(1.164)
,
(1.164)
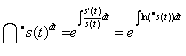 .
(1.164Ó)
.
(1.164Ó)
It is possible to conclude from the notions defined above that the harmonic unit, to within a constant factor C, is a multiplicative integral:
![]() .
(1.165)
.
(1.165)
7.5. Additive and multiplicative integrals
Additive and multiplicative derivatives and differentials provide for comprehensive description of complex judgements as superpositions of elementary judgements in the form both sums and products of various degree of discontinuity:
a) Additiveb) Multiplicative
1. discontinuous superposition
![]() ----
----![]()
2. discrete superposition
![]() ----
----![]()
3. indiscrete superposition
![]() ----
----![]()
4. continuous superposition
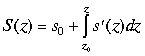 ----
----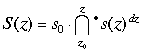
Multiplicative integrals are calculated on the basis of additive integrals and can be simpler and more complex than the latter, for example:
Additive integrals Multiplicative integrals
------![]() ---------------------
---------------------![]() -----------------
-----------------
------------![]() -----------------
-----------------![]() ----
----
-------------- -![]() -------------------
-------------------![]() ------(1.166)
------(1.166)
------------------![]() --------------
--------------![]() --------
--------
----![]() ----------------
----------------![]() ---------
---------
----![]() ------------
------------![]() ,----
,----
where ![]() is Lobachevsky's function.
is Lobachevsky's function.
Theoretical Dialectical Journal: Physics-Mathematics-Logic-Philosophy, N.1, site http://www.tedial.narod.ru/