L. G. Kreidik (translation from Russian T. S. Kortneva and G. P. Shpenkov)

13.1 Introduction

Objective and subjective times are two fundamental elements of the objective-subjective Universe, which are conserved, being non-conserved, because they partly pass from one level of the Universe to another, where, speaking figuratively, they are recorded as a time file of past events. It can be suggested that the files are contained in the genetic code of humans and everything that exists on the Earth. In accordance with this, we will write the oppositus of some process on an elementary wave of physical time . This procedure will result in the elementary differential of an information pulse:

, (2.309)

Its total measure will be assumed equal to the integral

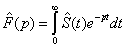. (2.310)

Within the dimensionality, the information pulse is an amplitude-modulated wave of physical time. If the information pulse is known, then according to (1.199) the oppositus is equal to the integral:

. (2.311)

The space of specific velocities is the inverse temporal space, in which the integral sum of the differentials of the inverse time field determines the event S(t) of the direct time field.

13.2. Exchange in terms of information pulses

The exchange that is described by the equation

. (2.312)

will be discussed in terms of information.

If the exchange is discrete initially, then the kinematic exchange has the form

. (2.313)

The first component here is a continuous part of the exchange, the second one indicates discrete stepwise involvement of the power, the third and fifth components describe a discrete jump of the displacement, and the fourth component exoresses a jump of the velocity. The initial displacement and velocity are assumed to be zero.

Using (2.310) and bearing in mind (2.313), we will write exchange (2.312) in terms of information pulses as

. (2.314)

Hence, the information pulse of the displacement will be

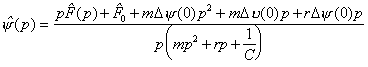. (2.315)

In terms of this information pulse, the oppositus of the displacement can be determined from (2.311).

We will consider the simple situation for the present:

, (2.316)

The information equation is

. (2.317)

Hence, the information pulse of velocity is

, where (2.318)

and the velocity is

, (2.319)

where factor 2 indicates doubling of the information as against classical calculation methods. In ordinary operational analysis integration is carried out over the whole half-plane of specific velocities, therewith contradiction of the process is artificially eliminated. In the present case, integration involves a quarter of the half-plane, conserving other 50% of information, which becomes doubled. Integral (2.319) is defined by the semi-circulations at the points and :

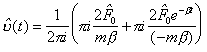. (2.320)

Finally, we have

. (2.321)

In contemporary mathematics, and, therefore, the oppositus describes motion alone. But the longitudinal kinetic field is associated with the transverse potential field and their velocities are equal. Consequently, it is necessary to assume .

A plot of motion-rest velocity is shown in Fig. 2.16. Certainly, it does not express the complete picture, since the longitudinal potential field is omitted here.

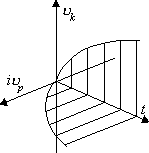
Fig. 2.16. A graph of motion-rest velocity.

If in (2.313) F(t) = 0 is assumed, the state of motion-rest will be described by the information pulse of displacement (2.315), which will be and therewith

, (2.322)

where , , and , there with and .

Using (2.322), we have

. (2.323)

The integral is equal to the sum of half-circulation at the point and the total circulation at the point :

.

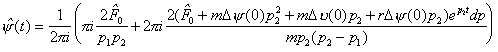Some simple manipulations result in

, (2.324)

where

. (2.325)

The elementary spatial displacement is proportional to the physical time, therefore arbitrary spatial displacements should also be proportional to the physical time.

We take a constant velocity of comparison as a proportionality factor, then

. (2.326)

13.3. An information pulse of time

Now, we will consider time exchange (2.312). Let, for example,

and . (2.327)

In view of (2.326), we have

(2.328)

or

. (2.328a)

The information equation of time will be

, (2.329)

From this equation, we find the information pulse of time

, (2.330)

where . The information pulse determines the time field:

. (2.331)

The integral is equal to the sum of half-circulation at the point and circulation at the point :

Eventually, we have

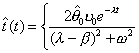
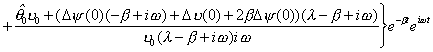(2.332)

The first component of the time field is aperiodic decaying time, the second component is periodic decaying time. At we have aperiodic resonance of time.

Physical time is a complex multidimensional ideal field of time, the elementary structure of which replicates the simplest triad of the field of rest-motion, i.e. it is characterized by the longitudinal and transverse time field of rest and the longitudinal time field of motion. Here, the kinetic time changes with the phase shift 90° to the longitudinal time and in the same phase with transverse potential time.

An elementary displacement is a contradictory process of rest-motion. Motion is the ideal state of rest, its another being. In turn, rest is the material state of motion, its another being. Consequently, physical time is contradictory material-ideal time, the material facet of which is potential time, whereas the ideal aspect of its is kinetic time.

Elementary kinematics of rest-motion was presented in this chapter. Against to classical tradition, motion and rest are concerned in close nonseparable contradictory relation. This dialectical bond are expressed by a dialectical material-ideal field of numbers and a binary set of notions. Every binary pair of the notions describes corresponging aspects of motion and rest giving opportunity to see both kinetic and potential sides of kinematics of real processes.

Description of dynamics has also dialectical binary character. The nonforce description of relations between objects, called as "exchange", differs in principle from the classical approach based on the notion of force interaction. "Exchange", in wide sense of this word, is here the exchange by motion, rest, space, material, arbitrary state, etc.

The laws of conservation-nonconservation (transformation) of any states and phenomena of nature, including time, but not Newton's laws, are the basis of the exchange.

Dialectics of rest-motion considers also time as a contradictory potential-kinetic field of time. In infinite space of the Universe, in accordance with the laws of conservation-nonconservation, the transformation of potential motion, i.e. rest, into kinetic motion, i.e. simply motion, and conversely is continuously occured. Moreover, if rest expresses some material facet of an object, then motion represents its ideal side. In that sense, potential-kinetic time is material-ideal time.

Transition of material time into ideal time and, inversely, ideal time into material, takes place at all levels of the Universe. Therewith, total quantity of time is invariable. The law of conservation alike with the law of non-conservation or transformation of time is valid here. Thus, time is conserved, being non-conserved. On the other hand, time is non-conserved, being conserved. The essense of the law of conservation and transformation of time is in that.

The above description of physical processes on base of the binary dialectical system of notions and the conservation-nonconservation laws is more effective then the force description at present. Such approach expands our understanding of the phenomena of nature and allows us relatively simply to solve problems which extremely hard to solve by the traditional way.

Theoretical Dialectical Journal: Physics-Mathematics-Logic-Philosophy, N.2, site http://www.tedial.narod.ru/