L. G. Kreidik (translation from Russian T. S. Kortneva and G. P. Shpenkov)

4.1. A center of mass of the system

All above parameters of motion-rest refer to the one material point and describe absolute displacement within the first term only. However, in description of a system of material points, apart from absolute motion-rest, there occurs relative motion-rest and displacement of the system is contradictory and absolutely-relative. Therefore, it seems useful to introduce absolute-relative parameters of motion-rest, using the center of mass of the system as a reference point.

The center of mass is a common, average, collective point of motion-rest of the system:

, where . (2.44)

4.2. A vector of configuration of the material point; a partial vector of the system

The absolute-relative position vector or configuration vector of the i-th material point of the system will be defined by the equality

,(2.45)

where , , and are different notations of the same absolute position or displacement of the point

.(2.46)

The second term expresses a relative position or displacement the point:

(2.47)

The position vector itself of the i-th material point will be called a partial vector of the system.

As follows from the definition (2.47), the partial vector of the system is equal to the configuration vector of the center of mass:

. (2.48)

The vector of relative configuration of the i-th material point expresses its position relatively to all material points of the system:

where the coefficients are

. (2.50)

These coefficients will be called relative masses. Components of the relative configuration vector are relative configurations of the i-th and k-th points.

4.3. A matrix of total configuration

In terms of the notions just defined, it is possible to express the absolute-relative configuration of the system by the total configuration matrix:

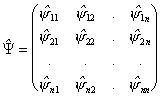. (2.52)

The spur of the matrix equal to the sum of its diagonal elements determines the absolute configuration of the system:

. (2.53)

Off-diagonal elements of the matrix, symmetric relatively to the diagonal, equal in value and opposite in sign, define the relative configuration of the system and the lines describe the absolute-relative configuration of the points.

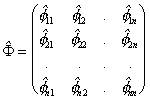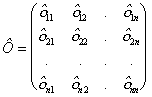, . (2.54)

4.4. State vectors of the material point

,(2.55)

where the vector of absolute state is

(2.56)

and the vector of relative state is

.(2.57)

The vector equal to the product of the mass of an arbitrary material point of the system by the position vector of the center of mass of the system will be called a partial vector of absolute-relative state of the system. As follows from the definition, the absolute-relative state vector of the z'-th material point is equal to the partial state vector of the system:

.(2.58)

The sum of all partial states of the system determines the state of the whole system:

(2.59)

4.5. A matrix of the system state

The state of the system can be conveniently described by the matrix of its state as

,(2.60)

where are diagonal elements of absolute state.

The spur of the matrix is equal to absolute state of the system and the relative state vector is zero. The state vector of the system is equal to its absolute state vector:

.(2.61)

This result is natural as the system by itself is unconditional and its relative state is zero.

4.6. Momentum of the material point and entire system

The derivative of absolute-relative state of the i-th material point defines its absolute-relative momentum

,(2.62)

where

(2.63)

is the absolute momentum of the i-th material point and

(2.64)

is the relative momentum of the i -th material point.

The total momentum of the material point is equal to the partial momentum of the system:

.(2.65)

The sum of the partial momenta of the system defines the momentum of the system:

. (2 66)

. (2.67)

4.7. Kinema of the system

The time derivative of the absolutely-relative momentum of the i-th material point determines its absolutely-relative kinema:

,(2.68)

equal to the partial kinema of the system

.(2.69)

The sum of partial kinemas of the system is equal to the kinema of the system:

.(2.70)

The derivative of the matrix of momentum of the system leads us to the matrix of the kinema:

. (2.71)

4.8. Mobilite of the system

The time derivative of the absolute-relative kinema of the i-th material point determines its absolute-relative mobilite:

;(2.72)

equal to the partial mobilite of the system

.(2.73)

The sum of partial mobilites of the system is equal to the mobilite of the system:

,(2.74)

which can also be expressed in a matrix form.

4.9. Measures of energy

Now we will consider absolute-relative energy of the system on the, defining it by the equality

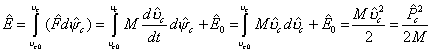. (2.75)

Separating the absolute and relative parts of the energy, we obtain

,(2.76)

where the absolute component of the energy is

,(2.77)

and the relative component is

.(2.78)

Relative motion is negation of absolute motion, therefore, a measure of the relative velocity can also be the quantity

,(2.79)

related with the relative momentum

.(2.80)

Using this form of the relative momentum, we can write the energy expression

(2.81)

or

(2.82)

The matrix form of absolute-relative energy is as follows:

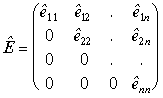.(2.83)

The matrix of absolute-relative energy is a triangle. The spur defines the absolute component of the energy and the sum of all diagonal elements is equal to the relative energy of the system. The total absolutely-relative energy of the system is equal to the sum of all elements of the matrix or, as will be said in the following, to the total spur of the matrix, which will be denoted by a capital letter:

. (2.84)

Thus, we will distinguish a total spur of the matrix and a partial or a diagonal spur.

The structure of the energy of the system on the other levels (see (2.41), (2.75) and (2.76)) is defined similarly. In particular, the -level energy is

.(2.85)

The first time derivatives of energy of the system are equal to absolute-relative powers.In particular, on the -level of motion-rest we have

(2.86)

or in the matrix form

.(2.87)

In a closed system, mutual transformation of absolute and relative motion is possible but the total motion is preserved.

4.10. The center of mass of the system in absolute-relative motion

Vectors of absolute-relative state of all points of the system define the absolute-relative structure of the center of mass of the system. According to (2.55), the vector of absolute-relative state of i-th material point has the following form

.

Taking it into account, the center of mass of the system in absolute-relative motion is defined as

.(2.88)

The absolute component of the center mass position of the system reflects its potential and kinetic sides, whereas relative component describes relative positions of points of the system. Therefore, the configuration matrix of the center of mass of the system gives complete information about the system.

The sum of diagonal elements of the matrix defines absolute aspect of the center mass position. Off-diagonal elements define the relative position of points and their total sum is equal to zero because relative positions of any two points are opposite by sign.

Theoretical Dialectical Journal: Physics-Mathematics-Logic-Philosophy, N.2, site http://www.tedial.narod.ru/