5. Laws of Conservation-Non-conservation of Exchange
L. G. Kreidik (translation from Russian T. S. Kortneva and G. P. Shpenkov)
5.1. A meaning of the conservation-non-conservation laws; a concept of exchange
In dialectics laws of conservation are impossible without laws of non-conservation. In a classical physics following Aristotle's rules, the word "non-conservation" is substituted by the word "transformation", making illusion of existence only the law of conservation.
In actual fact, the word "transformation" means that have place the change of an object and process, which continuously and discretely transfer in the different states. Therefore, dialectics makes it possible the conservation-non-conservation law to describe by any parameter of exchange and state.
Everything in the Universe is non-conserved, being conserved, and, being non-conserved, everything is conserved. This is the essence of the law of conservation-non-conservation.
All changes are related to exchange. The notion exchange is wider that the notion interaction since the interaction means the only concentrated exchange. However, exchange also occurs when we do not find any interaction. The ideal exchange is mainly the exchange by motion-rest, i.e. it takes place kinetic-potential exchange. The material exchange is going with mass exchange as well
5.2. Conservation-non-conservation in a system of two material points
We will consider conservation-non-conservation in the system of two material points. This system is characterized by absolute-relative motion-rest. For two different states of the system the law of conservation-non-conservation has the form
![]() .
(2.89)
.
(2.89)
The left-hand side of the equality is the state of the system
before exchange ![]() ,
the right-hand side includes the state of the system after exchange
,
the right-hand side includes the state of the system after exchange ![]() and the non-conservation term
and the non-conservation term ![]() which describes the transformed part of the state.
which describes the transformed part of the state.
On the level of momenta and energies, the law of conservation-non-conservation has a similar form:
![]() ,
,
![]() , (2.90)
, (2.90)
where P and G, E and W are momenta and
energies before and after exchange; ![]() and
and ![]() are
changes in the momentum and energy induced by motion-rest exchange with the
environment. The changes are usually positive and express scattering of motion-rest
into the environment. On a microlevel this scattering transforms into motion-rest.
If changes are negative, exchange is inverse and motion-rest passes from a microlevel
to a macrolevel.
are
changes in the momentum and energy induced by motion-rest exchange with the
environment. The changes are usually positive and express scattering of motion-rest
into the environment. On a microlevel this scattering transforms into motion-rest.
If changes are negative, exchange is inverse and motion-rest passes from a microlevel
to a macrolevel.
Energies of the system of two points, describing absolute-relative motion-rest before and after exchange and its transformation, are
![]() ,
,
------ ![]() (2.91)
(2.91)
and
![]() ,
,
where ![]() and
and ![]() are momenta
of points of the system before and after exchange.
are momenta
of points of the system before and after exchange.
5.3. Laws of conservation-non-conservation at discrete, impulse, exchange (a central impact)
Let rest-motion exchange between material points occurs in
this system. If the exchange is continuous and its duration is infinitesimal,
the energy losses ![]() tend to zero.
tend to zero.
If the exchange is discrete, closely to pulse, the energy losses on the macrolevel can differ substantially from zero.
Central impact is the simplest realization of discrete exchange. Conservation-non-conservation of momentum in central impact has the form
![]() ,
,
![]() , (2.92)
, (2.92)
where relative masses mn and m2] (see (2.50)) are determined by
![]() .
.
Since the sums of relative momenta are zero, then
---------![]() .
(2.93)
.
(2.93)
If the losses can be neglected, then
-------- ![]() . (2.94)
. (2.94)
In this case the partial momentum of the first material point is preserved:
---------![]() .
(2.95)
.
(2.95)
Let as introduce the ratio of relative momenta by
------![]() (2.96)
(2.96)
and equality (2.95) will be transformed to
![]() .
.
A similar equality also holds for the second point of the system:
![]() .
.
Hence, we have classical formulae for velocities after the impact:
-------![]() , (2.97)
, (2.97)
--------![]() . (2.98)
. (2.98)
Central impact is called absolutely elastic, if relative momenta
before and after the impact are equal in value and opposite in sign. In this
case ![]() and
and
---------![]() ,
,
![]() . (2.99)
. (2.99)
Since impact without losses is considered, the law of conservation of absolute-relative energy before and after the impact is also valid here:
![]()
or
![]() .
(2.100)
.
(2.100)
The first two terms left and right from the equality sign is absolute kinetic energies, the third negative ones are relative energies.
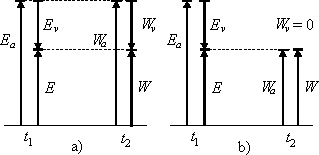
Fig.2.1. Diagrams of energy conservation with absolutely elastic impact (a) and absolutely inelastic (b); Ea and Wa are absolute energies, Ev and Wv are relative energies, E and W are total absolute-relative energies before and after exchange.
For absolutely elastic impact, absolute Ea and relative Ev energies are also conserved separately. The energy diagram of exchange (Fig.2.1) can easily present the results.
A central impact will be called absolutely inelastic, if relative momenta after
the impact are zero (![]() ).
After the impact, relative energy becomes zero. Absolute energy decreases by
the value of the relative energy loss but the signs of the energies are opposite,
therefore the total energy of the system is preserved:
).
After the impact, relative energy becomes zero. Absolute energy decreases by
the value of the relative energy loss but the signs of the energies are opposite,
therefore the total energy of the system is preserved:
![]()
or
![]() . (2.101)
. (2.101)
It should be emphasized that the value of the total lost energy is zero. Of course, disappeared parts of absolute and relative components of the total energy vanishing did not vanish, because, having vanished on the macrolevel, they will appear on the microlevel in the form of kinetic and potential energies. Since the signs of kinetic and potential energies are opposite, the total gained energy is also zero here. The motion-rest transformation process is not completed on the atomic-molecular level since motion-rest partially passes to the subatomic level, continuing its motion into the depth of the Universe through an infinite series of its levels.
In a general case, central impact is elastic-inelastic, i.e. it is contradictory discrete-indiscrete exchange. Its energy diagrams are shown in Fig. 2.2
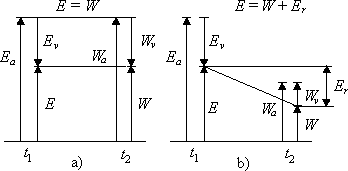
Fig.2.2. Diagrams of the law of conservation-non-conservation
energy in the case of elastic-inelastic impact, if ![]() (a) and
(a) and ![]() (b).
(b).
If in a system with any number of material points relative motion disappears, off-diagonal elements become zero, and diagonal elements become contradictory, kinetic-potential. In particular, the matrix of momenta becomes
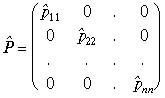 .
(2.102)
.
(2.102)
It is natural, since the diagonal matrix describes the absolute aspect of nature and the sum of the diagonal elements is conserved if there are no transformations.
Theoretical Dialectical Journal: Physics-Mathematics-Logic-Philosophy, N.2, site http://www.tedial.narod.ru/