Elementary dialectical kinematics and dynamics of exchange. The complete description of uniform movement on a circle absent in the classical mechanics

6. Kinematics-Dynamics of Rotational Rest-Motion of a Material Point

L. G. Kreidik (translation from Russian T. S. Kortneva and G. P. Shpenkov)

6.1. A potential-kinetic vector of circular motion

Kinematics and dynamics of rectilinear and rotational motions are still at the stage of development. Creation of an adequate by mature theory describing these motions will require great effort. Cognition of elementary kinematics-dynamics is impossible, neglecting symmetric-asymmetric motion and rest, which should be described together. Outstanding Russian artist N.N. Ge used to tell to his students: "You should never paint a part separated from the whole... Whenever you paint a part, paint it, bearing in mind the whole. Paint symmetric parts together and simultaneously". This seems true for physics and mathematics, too, because they produce logical, mathematical, and physical pictures of nature. For thorough dialectical description, we will have to expand the stock of terms used to denote the notions in kinematics and dynamics.

We will start from circular motion. For simplicity circular motion will be assumed plane and uniform. Let a material point move counterclockwise. This motion is complicated and consists of two mutually perpendicular potential-kinetic harmonic oscillation

-------- . (2.103)

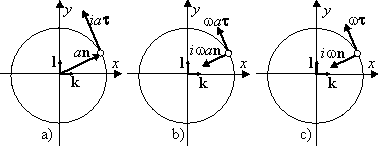
Fig. 2.3. Kinematics of circular motion-rest; a) is a potential vector of motion, is a kinetic vector of motion, b) is a potential velocity, is a kinetic velocity, c) is a potential specific velocity, is a kinetic specific velocity.

The minus sign at the kinetic displacement along the x-axis indicates the direction of the motion along this axis. Motion along the _y-axis is negation of motion along the x-axis:

. (2.104)

The potential-kinetic vector of circular motion of the point has the form (Fig. 2.3a):

, (2.105)

where k and l are unit vectors of x- and y-axis and

(2.106)

is a potential radius with the modus a, characterizing the constant potential aspect of rotational motion and directed along the radius-vector of the point; ;

(2.107)

is the kinetic radius with the modus ai, characterizing the variable kinetic aspect of rotational motion; it is perpendicular to the potential radius and directed along the tangent in the direction of circular motion.

Thus, the potential-kinetic vector f with the basis vectors and (Fig. 2.3a):

, where , . (2.108)

The complex modulus of the vector is .

A potential radius expresses the extent of occurrence and a kinetic radius, the extent of nonoccurrence of the material point at each point of the circular trajectory. A potential-kinetic radius determines simultaneously occurrence and nonoccurrence of the material point at every point of the circle. The modus of this vector in the fixed basis of the vectors k and l is equal to the sum of harmonic oscillation along the X- and j-axes:

, (2.109)

where is a complex modulus of the potential-kinetic radius .

6.2. A kinetic-potential velocity of circular motion

The derivative of the radius-vector defines the kinetic-potential velocity of circular motion (Fig. 2.3b):

, (2.110)

where is kinetic or tangential velocity in the direction of motion and is potential or normal velocity directed to the center of the circle.

The time derivative of the modus of the radius-vector in the fixed basis defines the modus form of the kinetic-potential velocity:

, (2.111)

where

(2.112)

is the complex modulus of velocity.

Kinetic velocity characterizes the quantitative aspect of motion and the qualitative aspect of rest, while potential velocity characterizes the quantitative aspect of rest and qualitative aspect of motion.

The field of velocity defines the field of specific velocity. In circular motion, the specific velocity is expressed by two forms, namely, scalar and vector. As a scalar, it is the potential-kinetic angle of turn of the potential-kinetic radius-vector of the point per unit time. As a specific vector, the velocity is defined as (Fig. 2.3c):

, (2.113)

where is the specific tangential kinetic velocity and is the specific normal or specific centripetal potential velocity. The modus form of the specific velocity in the fixed basis is defined as

, (2.114)

where

(2.115)

is the complex modulus of the specific velocity.

6.3. Flux and circulation in circular motion

The velocity vector defines the longitudinal-transverse kinematic flow through the circular trajectory of motion:

, (2.116)

where

(2.117)

is a transverse kinetic flow or circulation and

(2.118)

is a longitudinal potential flow.

The circulation and flow are closely related. It can be stated that a transverse kinematic flow is longitudinal circulation and a longitudinal potential flow is transverse circulation. The relation of velocity and circulation is similar to analogous notions in the theory of field:

. (2.119)

6.4. Flux density; rotorodivergence

Cognition is realized by comparison and impossible without comparison. Therefore, it seems useful to introduce the notion of flux density, equal to the ratio of the flux to the area of the circle bounded by the trajectory:

. (2.120)

The kinetic component of the flux density will be called a rotor component of the flux density or rotor of velocity:

. (2.121)

The potential component of the flux density is called a divergence component of the flux density or a divergence of velocity:

. (2.122)

The total flux density will be called a rotorodivergence and denoted символом

. (2.123)

6.5. Kinetic-potential momentum of a point at a circle

The kinetic-potential momentum of the point on the circle is

, (2.124)

where is a tangential or kinetic momentum and is a normal or centripetal potential momentum.

The structure of the kinetic-potential momentum and its modus form in the fixed basis are, respectively,

, (2.125)

. (2.126)

6.6. Specific momentum or kinetic-potential charge

As consistent with (2.124), the specific momentum or kinetic-potential charge is

. (2.127)

Its modus form in the mobile basis is

. (2.128)

In the fixed basis, the modus of the charge is

. (2.129)

It is evident that

. (2.130)

The product of the kinematic charge by the circle radius determines its kinematic moment equal to the momentum of the material point. The kinematic charge is related to the rotorodivergence of velocity and momentum:

, (2.131)

, (2.132)

where

, , (2.133)

, ,(2.134)

is the density vector of the transverse kinetic charge and is the density vector of the longitudinal potential charge.

6.7. Modus forms of rotor and divergence of momentum

Modus forms of the rotor and divergence of momentum are

, . (2.135)

In the above forms, rest is negation of motion but if algebra of rest is YES-algebra, algebra of motion is NO-algebra. Then,

, . (2.136)

This inversion holds for all the notions presented. Choice of the type of algebra depends on the nature of a concrete state or phenomenon. If one follows the nature of motion, potential displacements, i.e. ordinary displacements of material points, should be described by ideal numbers since the trajectories of the points are ideal lines, while material lines are systems of material points forming the lines.

6.8. Accelerations

The derivative of the potential-kinetic velocity determines the potential-kinetic acceleration:

, (2.137)

where

(2.137а)

is the potential acceleration.

(2.137b)

is the kinetic acceleration.

As per (2.137), the specific potential-kinetic acceleration has the form

. (2.138)

Modus forms of the accelerations in the fixed and mobile bases are

, , (2.139)

, . (2.140)

Potential normal or centripetal acceleration is directed to the center of the circle and kinetic tangential or rotational acceleration, in the direction opposite to the motion. The potential acceleration is quantitative and the kinetic acceleration is qualitative.

6.9. Kinema, mobilite and kinematic current

Kinema and kinematic current are equal to

, (2.141)

. (2.142)

The kinema defines the mobilite :

(2.143)

. (2.143a)

The structural and modus form of the kinema are

, , (2.144)

where .

A potential normal kinema is a centripetal quantitative kinema and a kinetic tangential kinema is a qualitative kinema, it has the direction opposite to the circular motion.

From formula (2.144), we obtain the structure and modus form of the kinematic current:

, . (2.145)

The kinematic current is potential-kinetic and longitudinal-transverse current. The kinema , current , and charge are related by the equality

, (2.146)

where is a modus of the potential velocity.

The rotorodivergence of the kinema defines the kinematic current:

. (2.147)

The rotorodivergence of velocit y is also relation to the acceleration, , the specific charge, , by

, (2.148)

where is a modulus of kinetic velocity.

6.10. Moments of momentum and kinema

Potential-kinetic moments of momentum and kinema will be defined by

, (2.149)

, (2.150)

where

(2.151)

is a centripetal potential moment and

(2.152)

is a tangential kinetic moment.

The ratio of the moment of kinematic charge to the moment of

momentum has the form

. (2.153)

6.11. Total energy of circular motion of a point

We will define the total energy of circular motion of the point

(2.154)

or . (2.154a)

Since the vectors and are mutually perpendicular, the third term of energy becomes zero and we have finally:

or , (2.155)

where is a kinetic moment of momentum and is a potential moment of momentum. Consequently, in circular motion potential-kinetic energy of a material point is zero.

6.12. Kinematic current in circular motion

Let us consider an important aspect of circular motion. Two points A and B will be taken on the circle (Fig. 2.4). They divided the circle by the two half-circle. Circular motion of the material points will be assumed uniform. The motion along the arc AmB and the reverse motion along thearc BnA occurs for the same time, equal to a half period T of circular motion.

Now, we will introduce a mass transfer current or a current of mass, flowing through the cross-section of a material trajectory (the cross-section is not equal to zero), according to:

, (2.156)

And will determine its in circular motion.

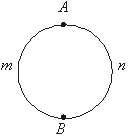
Fig. 2.4. The circle as a double-conductor line.

It is evident that the value of the current will not change, if the circle to stretch at the points A and B in a double conductor line (Fig. 2.4) and the velocity of motion to conserve the same. Thus, we will have a double-conductor line of mass exchange between the points A and B. The average current along AmB is

. (2.157)

In reverse motion along BnA the current will be of the same value. Now, the lines will be bent to form arcs and we go back to circular motion, mass current of which remained unchanged. Thus, the mass current in circular motion must be defined by (2.157). If mass is substituted by a kinematic charge , then we will have the charge current

. (2.158)

Of course, the procedure can be simplified. In any cross-section of the circular orbit, the moment of appearance of a material point will be taken as a reference time. After some time equal to the period, the point appears again in the cross-section, therefore, its passing through the cross-section should be countered twice. Consequently, the current will be defined by (2.158).

We have considered in detail this question because in the first decades of the 20th century the electric current generated by electrons on a circular orbit was assumed to be

, (2.159)

which is a serious error. We will return to this problem during analysis of electron behavior in space further.

When current in multiple processes is calculated from differential formula (2.156), all calculations will be equivalent; however, when unit effects are concerned, the approach should be extremely careful because it is easy to obtain inequivalent current. This logical error manifested itself in Einstein's and de Gaase's experiments. It was not eliminated and the theory was formally made consistent with experiment by introducing one error more in the form of the hypothesis of electron spin. Unfortunately, one error that shades another generates the illusive truth, taking science further from the truth.

Circular motion is contradictory as it is represented by a central field of rest and a circular field of motion. The field of rest is characterized by radial fields of potential displacement, potential velocity, and potential acceleration; the field of motion is characterized by circular fields of kinetic displacement, kinetic velocity, and kinetic acceleration (Fig. 2.5).

The trajectory of the field of rest-motion is a complex configuration consisting of a circular trajectory and its center. The circular trajectory is a contradictory structure of the potential circle with a radius a and a kinetic circle with the kinetic radius ia.

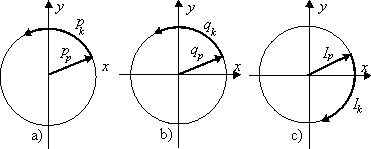
Fig. 2.5. The field of circular rest-motion of momentum , charge and current .

The equations of potential and kinetic circles

and (2.160)

give complete description of motion-rest on the geometric level.

The potential circle represents the material aspect of nature, while the kinetic circle represents its ideal aspect. In modern mathematics, where materialistic philosophy dominates, a kinetic circle in the field of complex numbers is represented by an imaginary circle and treated as an object that does not exist in nature.

The sum of potential and kinetic circles defines the kinetic-potential circle of a "zero" radius:

. (2.161)

expressing equilibrium of motion-rest.

6.13. Kinematics-Dynamics of Rectilinear Motion-Rest

If the circle radius tends to infinity, the arbitrary arc of the circle becomes a straight line. In this case circular motion becomes rectilinear (Fig. 2.6).

Any potential line segment / perpendicular to the straight line indicates possible positions of potential radii, corresponding to this rectilinear motion. The motion itself can be naturally characterized by the kinetic segment il directed along the motion.

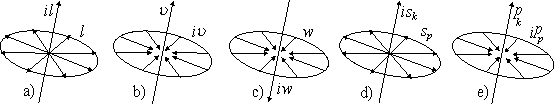
Fig. 2.6. Kinematics (a-c) and dynamics (d, e) of the field of rectilinear motion-rest; a) l+il is displacement, b) u +iu is velocity, c) w+iw is acceleration, d) is a state, e) is momentum.

An infinite set of potential radial rays to the straight line of the motion characterizes the field of potential-kinetic rectilinear motion (Fig. 2.6a). This field is longitudinally-transverse. Fields of velocity and acceleration have a similar structure (Fig. 2.6b,c). The structure of the state S and momentum P vectors (Fig. 2.6d,e):

, (2.162)

, (2.163)

and the other parameters of motion-rest performing circular motion is also the same. Evidently, all the above relations of circular motion are also valid for rectilinear motion. In particular, the relation between the moment of kinematic charge and the moment of momentum , defined by (2.153), holds here.

Potential-kinetic energy of the point in rectilinear motion is defined by formula (2.155). It is characterized by kinetic and potential energies, the total value of which is zero. It can be stated that transition from circular to rectilinear motion does not change the parameter values, which are completely conserved.

6.14. An Axial Field of Rest

Now we will go back to circular motion. Imagine an ideal plane with a small hole, through which a thin imponderable thread is pulled. One end of the thread is tied to a material point revolving around the hole over a circle with the radius a. This motion should be maintained by potential momentum equal to the kinetic one and directed along the axis of revolution to any side (Fig. 2.7). It should be emphasized that the plane of revolution has two sides, namely, a front side, on the surface of which revolution occurs counterclockwise, and a rear side, on the surface of which the revolution is clockwise. In real world these sides are note quivalent and the direction of potential momentum along the axis of revolution may determine the direction of possible motion both on micro- and macrolevels. An axial field of rest is localized on the axis of revolution and all potential radial parameters are a measure of this field (Fig.2.7).

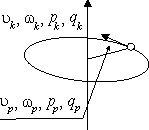
Fig. 2.7. A graph of a field of circular motion-rest

If the parameters to direct towards the side of clockwise revolution, they are equal to thecorresponding radial parameters within a unit radial vector. Since the direction, from the side of which motion of the material point is counter-clockwise, is considered to be a positive direction of the axis of revolution, the signs of parameters should be changed by inverse. Circular motion is a complex of fields: the axial field of rest and the longitudinal-transverse, or tangential-radial, field of motion-rest. A system of specific and linear parameters, or simply parameters, and their moments for the axial field is given as follows

a) velocity and specific velocity:---------------------- , ;