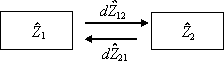
9. Kinematic-Dynamic Exchange
L. G. Kreidik (translation from Russian T. S. Kortneva and G. P. Shpenkov)
9.1. Kinematic exchange between two isolated systems (mutual exchange)
We will consider exchange between two isolated systems the states of which are characterized by a rest-motion parameter Z (Fig. 2.12).
Fig. 2.12. Exchange between two isolated systems.
The first system renders some of the rest-motion state ![]() to the second system and the second system renders the rest-motion
to the second system and the second system renders the rest-motion ![]() to the first one. Thus, changes in the state of the first and second systems
will be
to the first one. Thus, changes in the state of the first and second systems
will be
![]() ,
,
![]() (2.216)
(2.216)
and
![]() . (2.217)
. (2.217)
Hence, the exchange equation in terms of power becomes
![]() or
or ![]() , (2.218)
, (2.218)
![]() ,
,
![]() (2.219)
(2.219)
are the exchange powers, which are active, as exchange parameters,
but as parameters of ![]() -state,
they are passive. It is evident that
-state,
they are passive. It is evident that
![]() and
and ![]() . (2.220)
. (2.220)
Exchange is mutual, it is a channel with counter motion of
partial exchange components ![]() and
and ![]() . Their
values are unknown in a general case but their resultants
. Their
values are unknown in a general case but their resultants ![]() and
and ![]() . are known.
It should be emphasized that these differences are the same differential of
exchange, taken twice with opposite signs, since once the first system is taken
as a reference point and the second time, it is the second system.
. are known.
It should be emphasized that these differences are the same differential of
exchange, taken twice with opposite signs, since once the first system is taken
as a reference point and the second time, it is the second system.
In terms of forces, equality (2.218) is called the law of action and counteraction. This interpretation originates from naive thinking in terms of force. In the case of two weakly exchanging system, it can be physiologically perceived by a hand located between them. At the dawn of the natural science development, this sensation was given the name "force", which has varied its meaning in the course of centuries. This is, however, not exchange but a sensation of exchange.
If ![]() ,
the exchange equation becomes:
,
the exchange equation becomes:
![]() or
or ![]() . (2.221)
. (2.221)
In the language of dialectics, equation (2.221) states that
mutual exchange by the states ![]() and
and ![]() has the rate
has the rate
![]() , which is represented
once by the active exchange power
, which is represented
once by the active exchange power ![]() and the second time, by the active power
and the second time, by the active power ![]() .
.
In this exchange, the conservation conditions on the levels
![]() and
and ![]() are
valid
are
valid
![]() ,
,
![]() . (2.222)
. (2.222)
In terms of classical physics, it means that two systems interact
with momenta ![]() and
and ![]() equal in
value and opposite in direction, therewith they and "applied" to different systems.
equal in
value and opposite in direction, therewith they and "applied" to different systems.
If exchange arises on the level of ![]() -states,
then
-states,
then
![]() or
or ![]() (2.223)
(2.223)
and
![]() ,
,
![]() . (2.224)
. (2.224)
In this case classical physics states that two systems interact
with forces ![]() and
and
![]() equal in value,
opposite in direction, and applied to different systems.
equal in value,
opposite in direction, and applied to different systems.
In the sphere of objective dialectics there are no forces but
there is exchange by motion-rest on the level ![]() with power
with power ![]() .
On the other hand, exchange is the
.
On the other hand, exchange is the ![]() -level
of motion and
-level
of motion and ![]() and
and ![]() . are
parameters of state of motion. The exchange process is not completed here and
continues between
. are
parameters of state of motion. The exchange process is not completed here and
continues between ![]() -stages:
-stages:
![]() or
or ![]() (2.225)
(2.225)
and
![]() ,
,
![]() . (2.226)
. (2.226)
The fields ![]() ,
,
![]() ,
, ![]() and
and ![]() of states
and exchange are levels of a complex field of rest-motion. In a general case,
any parameter of exchange and state has continuous-discontinuous nature and
defined by
of states
and exchange are levels of a complex field of rest-motion. In a general case,
any parameter of exchange and state has continuous-discontinuous nature and
defined by
![]() , (2.227)
, (2.227)
where the first term in the right-hand side is continuous derivative describing continuous power of exchange and the second term is discrete derivative describing discrete power of exchange. Discrete exchange is widely spread. Impact is an example of it.
9.2. Dynamic exchange between two isolated systems (material exchange)
Now, we will consider material exchange or mass exchange or dynamic exchange. Let only mass exchange occur. Then, the dynamic momentum of mass exchange is
![]() , (2.228)
, (2.228)
where
![]() (2.229)
(2.229)
- here is the mass exchange power.
The power of mass exchange will be called dynamic charge. A dynamic charge formula has the same structure as the kinetic charge formula and supplements the latter at description of kinematic and dynamic exchanges. Mass exchange momentum or dynamic momentum is a monopole moment of dynamic charge.
The total dynamic-kinematic momentum in harmonic oscillation becomes
![]() or
or ![]() , (2.230)
, (2.230)
where qm is the dynamic charge, ![]() is
the kinematic charge. We can therefore write
is
the kinematic charge. We can therefore write
![]() , (2.231)
, (2.231)
where
![]() . (2.232)
. (2.232)
Here, the momentum describes a material-ideal field of exchange
and it is :haracterized by the total dynamic-kinematic charge ![]() .
A more general formula for the total momentum is
.
A more general formula for the total momentum is
![]() . (2.233)
. (2.233)
Assuming the dynamic charge to be constant, we will determine the total dynamic-kinematic kinema
![]() and
and ![]() , (2.234)
, (2.234)
where ![]() is the dynamic kinema or kinema of Mescherski [1,2],
is the dynamic kinema or kinema of Mescherski [1,2], ![]() is the kinematic kinema or kinema of Newton.
is the kinematic kinema or kinema of Newton.
Moments of dynamic momentum and kinema are similar in form to kinematic moments. It is evident that the ratio of dynamic moment of charge to the kinematic moment of momentum is
![]() . (2.235)
. (2.235)
This is also valid for circular motion.
Theoretical Dialectical Journal: Physics-Mathematics-Logic-Philosophy, N.2, site http://www.tedial.narod.ru/