STRUCTURE OF SPACE OF THE UNIVERSE
L. G. Kreidik,
Dialectical
Translation from Russian - T.S. Kortneva and
G. P. Shpenkov
1. A General Structure of the Universe
1.1. Levels
of matter states
Two extreme viewpoints exist in philosophy and science
about the general structure of the Universe: matter has a lower limit of its
divisibility or, alternatively, there is no
lower limit and matter is infinitely divisible. Philosophy of finite divisibility
has yielded a lot of unsolvable problems, therefore,
there are not grounds to consider this concept ultima
ratio. This problem needs dialectical interpretation.
The Universe is, first of all, a complicated contradictory
system that cannot be treated in the context of formal logic. Dialectics states:
the Universe is infinitely-non-infinitely divisible. This is a general statement that pertains not only to
matter. Let us elucidate the essence of this contradiction.
In physics, the principle of finite divisibility of microstructures predominates, whereas in mathematics,
it is adopted mainly the principle of infinite divisibility. Both principles
coexist quietly since their paths do not cross. Not infrequently during discussion
in one branch of science, these principles cause heated debates which can
be settled in form of dualistic solutions with great difficulty.
The concept of existence of the last indivisible state
of matter excludes the possibility of any exchange without which this state
cannot be a basis for the formation of overlying non-elementary states. If
we assume each state of matter to be elementary for overlying states and complicated
for underlying states, then the problem of interdependence of different states
of matter is naturally solved without any mathematical combinations. Under
such approach, there is no point in consideration of motion in vacuum as pure
mathematical nonexistence since any state of matter moves in the space of
underlying states and when the velocities are high, i.e. they approach to
wave speeds, it is necessary to take into account the nonlinear nature of
rest-motion and exchange.
The base of all levels of matter states are wave fields.
Therefore, motion is the complicated wave process of space-time and a simple
mechanical displacement can not exist here. In due course, quantum mechanics collided with this dilemma and had attempted
to solve its by the uncertainty principle.
Material states are closely related to the spectrum of
ideal states of the Universe. Both spectra form a single-nonsingle complex
of the states of the material-ideal Universe. Saying about the Universe,
we understand the entire Cosmos, i.e. all Galaxies and intergalactic objects
together with the Space and everything beyond their limits. Thus, Cosmos and
the Universe are synonyms here. Apparently, the Universe has a definite structure
and Galaxies form particular Worlds of the Cosmic level.
1.2 Dialectics of zero and infinity
Dialectics of infinite divisibility-indivisibility is closely related to
the dialectics of zero and infinity. We consider the Universe as the limiting
infinity. This infinity is termed the absolute or permanent infinity and designated
by 
.
If some arbitrary volume 
, confined by a closed surface, is chosen in the absolute
infinity, then the other part of the Universe represents the relative or
variable infinity 
, 
.
An infinite series of variable infinities tends to the absolute infinity
if arbitrary volumes, enclosed into one another, tend to zero:
. (3.1)
Consequently, the absolute infinity is closed by zero.
In this sense, zero and infinity represent two sides of the same facet of
the Universe.
Now, we consider the infinite divisibility
of matter deep into, approaching to zero (Fig. 3.1a).
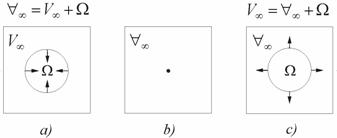
Fig. 3.1. Division depth into matter (a), transition through zero (b), division in
breadth after transition through zero (c).
Geometrically, each stage of the divisible matter will
be represented as a quasispherical volume with a set of normal vectors directed inside the
divisible volume. We will assume that each volume represents a motator pertaining to a particular level. Then, a transition
from one volume to another is the transition from one level of motators to another, more disperse, level. In such division,
the volume will be finally closed by zero (Fig. 3.1b), being a last brick
of the division. At the same time it is not the last brick because continuing
the division further we pass mechanically through zero; the volumes
of the division will already increase and the normals
will fall outside the external part of the volume (Fig. 3.1c). This process is the division in breadth. Thus, for
zero, the motators are the states of exchange and
in this respect the last level of division does not exist. Obviously, different
levels of the matter state are characterized by the different probability
of realization and, consequently, stability.
After passing through zero, the -
volume begins to increase (Fig. 3.1c) and the variable infinity will exceed
the absolute one by this volume:
. (3.2)
Equality (3.2) allows us to consider the absolute infinity as a period
of relative infinities, i.e. in a general case the formula of the variable
infinity becomes
, where 
. (3.3)
Hence, with the accuracy to a period, we have
or 
. (3.4)
Thus, the -volume, being smaller than the entire , can be
larger than it but we do not know about this. In particular, an electron may
be smaller and may be larger than an infinite period. The logic of infinity
expressed by formula (3.1)-(3.2) states that the inexhaustible is also exhaustible.
1.3. Dimension
of space
The structure of matter levels of the Universe, as the
contents, is inseparably linked with the structure of their spaces, as the
forms. The structure of motator levels is multidimensional.
A real space is multidimensional as well, but this multi-dimensionality is
not identical to the formal mathematical multidimensionality. Mathematics
deals with the infinite three-dimensional space which is described, as a rule,
by the infinite rectangular coordinate system. This subjective space does
not allow the fourth axis to be perpendicular to it. But the real Universe
consists of a set of objects with their confined spaces, providing thus the
physical multidimensionality.
In dialectics, the real space is described by material
and ideal points. The ideal point is zero-dimensional, while the material
point is three-dimensional.
Ideal points can form an ideal one-dimensional line,
whereas material points form the material four-dimensional line. Midpoints
of a cross-section of the material line with the coordinates determine the
longitudinal ideal axis of the material line.
(3.5)
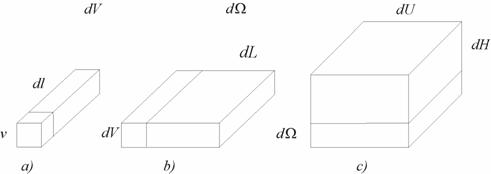
Fig. 3.2. Physical
volumes
The product of the three-dimensional volume 
of the material
point, forming this line, by a length of the line axis 
is termed a measure of the elementary four-dimensional volume of the material
line (Fig. 3.2a):
. (3.6)
Naturally, this measure is not single.
The ideal line, moving in space, forms a two-dimensional ideal surface.
The material line, recurring many times, forms a five-dimensional material
surface. Its volume is equal to the transverse product (see (1.29)) of the volume of material line 
by the line 
along
which the displacement takes place (Fig.3.2b)
, (3.7)
where 
is the angle formed
by the normal to the axis of the four-dimensional line and the direction of
the line 
.
Replicating in space, the ideal surface forms a three-dimensional volume;
the material surface makes up a six-dimensional volume equal to the transverse
product of a five-dimensional surface 
by the
length 
of
the line of the displacement (Fig. 3.2c):
, (3.8)
where 
is
the angle formed by the normal to the five-dimensional surface and the direction
of the line .
In successive recurrence, the six-dimensional formation, as a material
point, will form, like its primogenitor, a seven-dimensional line in space.
A set of the seven-dimensional lines forms an eight-dimensional surface which
generates a nine-dimensional volume. Everything will be repeated again in
the sequence:
point - line - surface - volume
with measures of the types of
, 
, 
, 
.
The sign "
" above
letters points to the contradictory potential-kinetic nature of volumes
Thus, a volume of 
-dimensional space
is not only an additive but also a multiplicative quantity that is determined with an accuracy to the multiplier of
infinite dimensionality. The dimensionality itself represents a periodic quantity
with a fundamental period of three.
In practice, the deep components of the
absolute volume are omitted and the multiplicative differentials
,
,
, 
,
or
,
,
,
,
are employed
Here, 
is
a measure of volume ;
,,, are the zero-, one-, two-, three-dimensional volumes, correspondingly.
Zero-dimensional volumes are numbers. A numerical field
forms the zero-dimensional space which is nonseparable related to the -dimensional material-ideal
space.
The zero-dimensional space is the ideal quantitative qualitative field of the Universe localized outside
the space of the Universe and at the same time inside it. It could be thought
that the dialectical off-space quantitative-qualitative field is one of the
languages of the Eternity participating in linking the past and future, the
death and immortality. The off-space quantitative-qualitative numerical field
and the space field of the Universe together with the time space-field form
a single-nonsingle fundamental contradictory form
of its existence.
The off-space quantitative-qualitative field is internally multidimensional. This peculiar feature
of the quantitative-qualitative field allows us adequately to describe the
wave spaces of the Universe.
Now we give some examples
of concrete multidimensional objects in the light of dialectical understanding
of multidimensionality. We use the rectangular three-multidimensional coordinate
system as a reference system to describe multidimensional structures. Let
us consider the equation:
, (3.9)
where 
is the symbol of the impracticable operation of addition
realizing a
kinetic joint of a three-dimensional
spherical volume of a radius 
with
a point
,
, 
,
and
is
a variable radius whose values pertain to some interval of quantitative
values : 
(Fig.3.3a)
In this case, the realizable sum of three squared variables
describes the sphere with the radius . The
point above it is the fourth dimension.
Let changes in the interval
,then we
have a three-dimensional sphere with the perpendicular of the length
erected
to it which represents the fourth dimension for the three-dimensional sphere
(Fig. 3.3b). Now, we construct the five-dimensional
formation:
, (3.10)
where 
, with
and 
This object is a sphere with a circumference at the same
centre (Fig. 3.3c). Such five-dimensional formations
fill the Universe: a star and the orbit of its planet, a planet and the orbit
of its satellite.
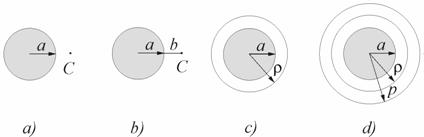
Fig. 3.3. A sphere
and the point C above (a), the sphere and the perpendicular b to it
(b), the sphere and a circumference (c), the sphere with two circumferences
(d).
A seven-dimensional object of the type:
, (3.11)
where
,
pertains to a
sphere with two circumferences at the same centre (Fig. 3.3d). In the Solar
system, such a formation is represented by Mars and two orbits of its satellites.
The above examples illustrate rather clearly the dialectical
understanding of multidimensionality. The structure of equations describing
multidimensional objects consists of separate components interlinked by the
signs of unrealizable addition. Each component in the equation describes a
subspace of the multidimensional space of a complex object. In a simplest
case, the dimensionality of the subspace is 
. In a general case, the equation of a subspace is as
follows:
. (3.12)
It is pertinent to note that the geometry of the object described by Eq. (3.12) is determined both
by the structure of the equation and the algebra of the variables.
1.4. Boundary
surfaces of space
The Universe has not boundaries and at the same time
it has them. The infinite part of the Universe is represented by the infinite
space, while its objects represent its finite part. For instance, the internal
space of an electron does not belong to the Universe, this is the external
side of the Universe and the electron surface is a boundary of the Universe.
In this sense, any electron is one of the terminations of the Universe. Dialectical
judgements of this kind are not a pun. Let us imagine that
a drop of a liquid is in a space craft in an imponderable state. The drop
may contain air bubbles inside it. This drop has the external spherical boundary
and the internal boundary represented by spherical surfaces of the air bubbles,
the internal space of which does not belong to the drop space. We speak about
the Universe in this natural sense as well.
Thus, an infinite series of motators
of the Universe is simultaneously an infinite series of the levels of its
terminations. In particular, atoms and molecules are at the same time atoms
and molecules of the inner boundaries of the Universe. The inner boundaries
are enclosed into each other. For instance, the inner space of any star, planet
and satellite is the outer space of the Universe and their surfaces are the
boundaries of the Universe, which consist of a set of microboundaries,
namely, molecules, atoms, nucleons, electrons,
and other microstructures. In other words, any objects in the Universe are
simultaneously its inner terminations, whereas it has no the external boundary
because the Universe is infinite. However, there is a contradiction also here:
the infinity is closed by zero and, consequently, any ideal point in the Universe
expresses the infinite boundary of the Universe.
