Theoretical Dialectical Journal: Physics-Mathematics-Logic-Philosophy
English-Russian
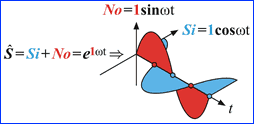 |
|
Issue
1
Contents
full text>
HTML-format
PDF-format
Dialectical Academy, Russia-Belarus
If there are questions and wishes, please send to L.G. Kreidik
Copyright ® L.G.Kreidik , 2001-2004