6. Непрерывные и прерывные дифференциалы и производные суждений диалектической логики
Л. Г. Крейдик
6.1. Материальная и идеальная точки
Корректное описание объективно-субъективных процессов опирается на понятие материальных и идеальных точек.
Идеальной точкой xi называем предел последовательности вложенных объемов материальных точек, когда их наибольший поперечник стремится к нулю. Положение идеальной точки определяется ее математическими координатами; в частности, если точка лежит на оси, ее координату и самую точку обычно будем обозначать одним и тем же символом типа xc.
Материальная точка xm - любой объект весьма малого объема, размеры которого необходимо принимать во внимание.
Положение материальной точки
и ее размеры выражаем с помощью ее произвольной идеальной точки; в частности,
если материальная точка лежит на оси, ее положение и размеры будем представлять
в виде интервала ![]() ,
где xc - некоторая идеальная
точка материальной точки xm. Таким
образом, в случае линейной материальной точки имеем
,
где xc - некоторая идеальная
точка материальной точки xm. Таким
образом, в случае линейной материальной точки имеем
![]() .
(1.106)
.
(1.106)
В тексте, ради краткости, материальную точку также будем обозначать символом ее идеальной точки xc.
6.2. Аддитивные дифференциалы
Взаимные аддитивные параметры точек и соотношения в пределах материальных точек выражаем аддитивными дифференциалами. Различаем четыре основных типа дифференциалов:
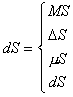 .
(1.107)
.
(1.107)
Первый прерывный, интегральный
дифференциал ![]() описывает конечные вариации, второй дискретный
описывает конечные вариации, второй дискретный ![]() - небольшие вариации, третий кретный
- небольшие вариации, третий кретный ![]() - малые вариации, четвертый непрерывный
- малые вариации, четвертый непрерывный ![]() - переменные вариации, принимающие любые сколь угодно малые значения, включая
и ноль в соответствующей точке суждения. Конечно, такое деление дифференциалов
на типы носит относительный характер.
- переменные вариации, принимающие любые сколь угодно малые значения, включая
и ноль в соответствующей точке суждения. Конечно, такое деление дифференциалов
на типы носит относительный характер.
Аддитивные вариации (дифференциалы) дополняем обратными аддитивными вариациями-дифференциалами в произвольной точке t:
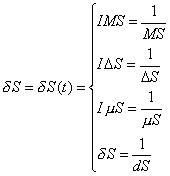 .
(1.108)
.
(1.108)
и в определенной точке ![]() :
:
![]() ,
(1.109)
,
(1.109)
где tk
- некоторая характерная идеальная точка материальной точки ![]() .
.
6.3. Аддитивные производные
Обобщенная аддитивная производная определяется выражением
![]() ,
(1.110)
,
(1.110)
где ![]() и
и ![]() дифференциалы любых типов и
дифференциалы любых типов и ![]() обратный дифференциал. Если дифференциалы непрерывны, предел отношения
обратный дифференциал. Если дифференциалы непрерывны, предел отношения
![]() (1.111)
(1.111)
определяет непрерывную производную. Дифференциалы одного типа образуют средние производные, дифференциалы не одного типа определяют производные различной степени дискретности:
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() , (1.112)
, (1.112)
где ![]() - некоторое малое приращение аргумента t.
Такие производные называем прерывными, дискретными, кретными и т.п.
- некоторое малое приращение аргумента t.
Такие производные называем прерывными, дискретными, кретными и т.п.
Материальные и идеальные точки, в которых суждение имеет непрерывную производную, есть точки непрерывного изменения или непрерывного перехода. Материальные точки с прерывными производными определяют точки прерывного изменения или перехода. Прерывные производные выражаем в следующей форме:
![]() ,
(1.113)
,
(1.113)
где ![]() - изменение переменной t в пределах
материальной точки прерывного перехода суждения и
- изменение переменной t в пределах
материальной точки прерывного перехода суждения и ![]() - обратный дифференциал. Когда материальная точка стягивается в идеальную, получаем
идеальную прерывную производную.
- обратный дифференциал. Когда материальная точка стягивается в идеальную, получаем
идеальную прерывную производную.
6.4. Характер изменения суждений
Производные, как оппозиты-суждения, позволяют высказывать суждения относительно характера изменения суждения, которое наглядно представляется графиками оппозиты и ее производной.
Нас будут интересовать, прежде всего, точки, в которых суждения претерпевают изломы и скачки, выражающие прерывно-непрерывные переходы в природе. Пусть суждение-оппозита в материальной точке xm претерпевает прерывный переход на качественной стороне и непрерывный на количественной стороне. Графически это выражается изломом (рис.1-10).
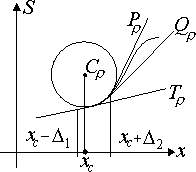
Рис.1-10. Оппозита и ее производная в области излома.
Суждение с изломом представляем логической конструкцией:
![]() ,
(1.114)
,
(1.114)
где ![]() и
и ![]() - оппозиты, определяющие поведение суждения
- оппозиты, определяющие поведение суждения ![]() до и после перехода;
до и после перехода; ![]() и
и ![]() - ступенчатые единичные суждения:
- ступенчатые единичные суждения:
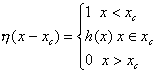 ___
___ 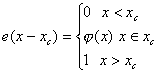 ,
(1.115)
,
(1.115)
где ![]() и
и ![]() функции в точке.
функции в точке.
Ступенчатые суждения описывают резкие переходы соответственно от 0 до 1 и от 1 до 0 в пределах материальной точки.
Такие переходы в зависимости от степени их крутизны называем прерывными, дискретными, кретными. Это реальные противоречивые переходы, дискретность которых реализуется через непрерывность. Если материальная точка трансформируется в идеальную точку, ступенчатые суждения переходят в идеальные ступенчатые суждения. Поведение функции (1.114) представляем упрощенной моделью
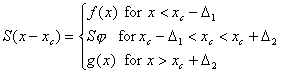 ,
(1.116)
,
(1.116)
где ![]() - некоторая предельная точка материальной точки перехода размером
- некоторая предельная точка материальной точки перехода размером ![]() и
и ![]() - значения принимаемые суждением в пределах точки перехода, которые лежат на
дуге круга
- значения принимаемые суждением в пределах точки перехода, которые лежат на
дуге круга ![]() радиуса
радиуса ![]() ,
символизирующего материальную точку графика суждения (рис.1-10).
,
символизирующего материальную точку графика суждения (рис.1-10).
Полагаем значения суждения слева и справа от точки излома равными значению суждения в самой точке излома, с точностью до вариаций суждения в пределах этой точки:
![]() ,
(1.117)
,
(1.117)
причем значения производных слева и справа от точки xm не равны:
![]() .
(1.118)
.
(1.118)
При малом радиусе ![]() суждение
суждение ![]() имеет в материальной точке xm
имеет в материальной точке xm
а) левую производную,
определяющую наклон касательной ![]() :
:
![]() ;
(1.119)
;
(1.119)
б) правую производную, определяющую наклон касательной ![]()
:
![]() ;
(1.120)
;
(1.120)
в) множество промежуточных производных,
значения которых непрерывно заполняют интервал ![]() ,
и определяют множество наклонов промежуточных касательных
,
и определяют множество наклонов промежуточных касательных
![]() :
:
![]() .
(1.121)
.
(1.121)
В материальной точке излома производную можно представить функциональной конструкцией:
![]() ,
,
![]() , (1.122)
, (1.122)
где
![]() - скачек производной. Во всем интервале изменения суждения имеем:
- скачек производной. Во всем интервале изменения суждения имеем:
![]() (1.123)
(1.123)
где первое и третье слагаемое определяют изменение производной до и после скачка.
Если положить:
![]() ,
(1.124)
,
(1.124)
тогда
![]() .
(1.125)
.
(1.125)
Здесь первое слагаемое - непрерывная
составляющая производной вне материальной точки ![]() .
Второе слагаемое определяет дискретную составляющую производной в пределах материальной
точки. Таким образом, производная, определяемая формулой (1.125), есть непрерывно-прерывная
производная.
.
Второе слагаемое определяет дискретную составляющую производной в пределах материальной
точки. Таким образом, производная, определяемая формулой (1.125), есть непрерывно-прерывная
производная.
Если производная ![]() не имеет в материальной точке излома, т.е. ее производные слева и справа равны:
не имеет в материальной точке излома, т.е. ее производные слева и справа равны:
![]() ,
тогда вторая производная в материальной точке принимает вид
,
тогда вторая производная в материальной точке принимает вид
![]() .
(1.126)
.
(1.126)
6.5. Обобщенный обратный дифференциал
Так как средняя производная ступенчатого единичного суждения в материальной точке xm равна обратному дифференциалу:
![]() ,
где
,
где ![]() (см. рис.1.5), (1.127)
(см. рис.1.5), (1.127)
то имеет смысл ввести обобщенный
обратный дифференциал, определяя его как обратный дифференциал-функцию ![]() ,
равный производной ступенчатого единичного суждения в материальной точке xm:
,
равный производной ступенчатого единичного суждения в материальной точке xm:
![]() .
(1.128)
.
(1.128)
Таким образом, можно говорить о двух обратных дифференциалах: дифференциале - средней производной и дифференциале - мгновенной производной в материальной точке xm. В дальнейшем, ради простоты, обратные дифференциалы обоих типов называем просто обратными дифференциалами. Когда материальная точка xm стягивается в идеальную точку xc, обратный дифференциал-функция обращается в идеальный предельный обратный дифференциал, равный d -функции.
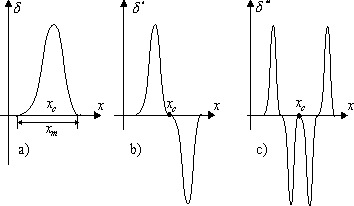
Рис.1-11. Обратный дифференциал и его первые две производные
Оперируя обратным дифференциалом, представим вторую производную суждения в материальной точке в виде:
![]() .
(1.129)
.
(1.129)
График обратного дифференциала-функции, имеющий вид весьма сжатого импульса, полностью определяет изменение n-ой производной в точке xm, если отсутствуют изломы производных:
![]() .
(1.130)
.
(1.130)
На рис.1-11 представлены графики
обратного дифференциала-функции и его двух первых производных, которые с точностью
до постоянного множителя ![]() показывают характер изменения производных в точках чистого излома, описываемого
на основе предложенной упрощенной модели излома.
показывают характер изменения производных в точках чистого излома, описываемого
на основе предложенной упрощенной модели излома.
6.6. Полная производная суждения
При ![]() семейство оппозит S со своими производными
переходит в оппозиту с идеальным абсолютно острым изломом (рис.1-12).
семейство оппозит S со своими производными
переходит в оппозиту с идеальным абсолютно острым изломом (рис.1-12).
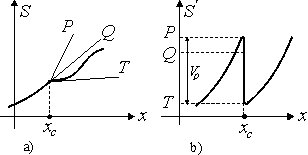
Рис.1-12. Функция и ее производная в области идеального излома.
В точке идеального математического излома оппозита имеет:
a) левую производную, определяющую наклон касательной ![]() :
:
:
![]() ;
(1.131)
;
(1.131)
б) правую производную, определяющую наклон касательной ![]() :
:
:
![]() ;
(1.132)
;
(1.132)
в) множество промежуточных производных,
значения которых непрерывно заполняют интервал ![]() и
определяют множество наклонов промежуточных касательных
и
определяют множество наклонов промежуточных касательных ![]() :
:
![]() .
(1.133)
.
(1.133)
.
Если в материальной точке выполняются условия:
![]() и
и ![]() (1.134)
(1.134)
суждение претерпевает дискретный переход с дискретной производной в точке перехода:
![]() где
где ![]() . (1.135)
. (1.135)
Такой переход называем скачком в материальной точке (рис.1-13). В нем имеет место неформальная количественная прерывность и качественная непрерывность.
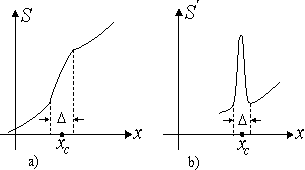
Рис.1-13. Функция и ее производная в области скачка.
Полная производная суждения со скачком имеет вид:
![]() ,
(1.136)
,
(1.136)
где ![]() - непрерывная и
- непрерывная и ![]() - прерывная составляющие полной производной. Соответственно
- прерывная составляющие полной производной. Соответственно ![]() -я
производная скачка имеет вид:
-я
производная скачка имеет вид:
![]() .
(1.137)
.
(1.137)
Сложный дискретный переход - скачок с изломом (рис.1-14) - характеризуется условием:
![]() и
и ![]() .
(1.138)
.
(1.138)
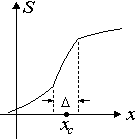
Рис.1-14.Скачок с изломом.
В нем первая производная содержит одно непрерывное слагаемое и два дискретных слагаемых, определяющих качественную и количественную дискретность:
![]() .
(1.139)
.
(1.139)
Дифференцируя первую производную, находим вторую:
![]() .
(1.140)
.
(1.140)
и т.д.
Отметим также следующие типы дискретностей:
а) двойной скачок - импульс ( рис.1-15а ):
![]() ,
,
![]() и
и ![]() , (1.141)
, (1.141)
б) импульс с изломом ( рис.1-15b ):
![]() ,
,
![]() и
и ![]() , (1.142)
, (1.142)
в) импульс со скачком ( рис.1-15c ):
![]() ,
,
![]() и
и ![]() , (1.143)
, (1.143)
г) импульс с изломом и скачком (рис.1-15d):
![]() ,
,
![]() и
и ![]() . (1.144)
. (1.144)
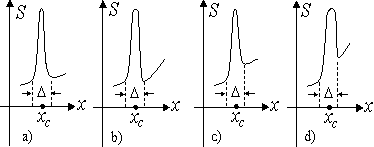
Рис.1-15. Дискретные переходы.
По мере того как растет поперечник материальной точки, прерывность ² растекается² , превращаясь в непрерывность.
Theoretical Dialectical Journal: Physics-Mathematics-Logic-Philosophy, N.1, site http://www.tedial.narod.ru/